Задача № 5.132.

Частица находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками (). Определить вероятность нахождения частицы с наименьшей энергией в области .

Решение:

Вид потенциальной ямы, в которой находится частица, представлен на рисунке 1:

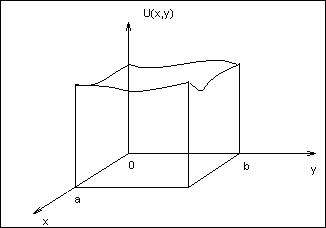
Рисунок 1

Потенциальная энергия имеет вид:

Составим уравнение Шредингера для области :

(1)

Или в виде:

(2)

где . Решение этого дифференциального уравнения имеет вид:

(3)

Пси-функция, описывающая состояние квантового объекта в потенциальной яме, должна удовлетворять стандартным условиям, накладываемым на пси-функцию: непрерывность, гладкость, конечность, однозначность. Воспользовавшись условием нормировки, имеем:

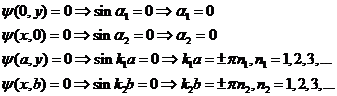(4)

Таким образом, пси-функция примет вид:

(5)

Найдём вторые производные пси-функции (5) и подставим в уравнение Шредингера (2):

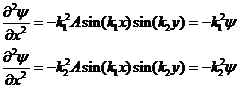(6)

Откуда, учитывая, что , получим:

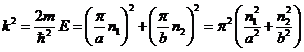(7)

Из выражения (6) определим энергетический спектр частицы:

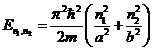(8)

Как видно из выражения (7) энергия частицы зависит от двух квантовых чисел и . Минимальная энергия частицы в данной потенциальной яме (при ) равняется:

(9)

Определим в выражении (5) для пси-функции, описывающей состояние частицы в потенциальной яме данного вида, постоянную А, используя условие нормировки пси-функций:

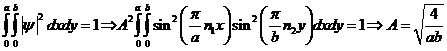(10)

Таким образом, пси-функция примет вид:

(11)

В состоянии с минимальным значением энергии квантовые числа равняются:

. В этом состоянии пси-функция равняется:

(12)

Графически эта пси-функция состояния частицы, в котором она имеет минимальную энергию, представлена на рисунке 2:

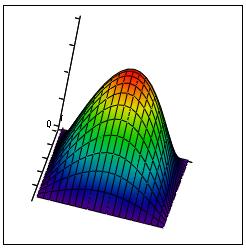
Рисунок 2

Как видно из рисунка пси-функция не удовлетворяет условию гладкости на границах области . Всё дело в том, что потенциальная яма с бесконечно высокими стенками – это идеализация реальной потенциальной ямы с высокими, но не бесконечными стенками. В результате мы и получили пси-функцию, которая удовлетворяет условию непрерывности, но не удовлетворяет условию гладкости.

Физический смысл пси-функции состоит в том, что квадрат модуля пси-функции определяет плотность вероятности нахождения частицы. Таким образом, плотность вероятности нахождения частицы в состоянии, в котором она имеет минимальную энергию, равняется:

(13)

Графически распределение плотности вероятности представлено на рисунке 3:

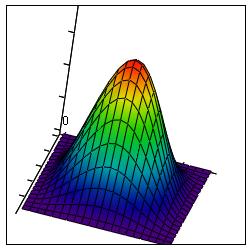
Рисунок 3

Вероятность нахождения частицы в области равняется:

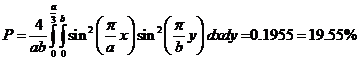
Ответ: Вероятность нахождения частицы в области равняется .