Задача № 5.149.
Электрон в атоме водорода в ![]() -состоянии описывается волновой функцией, радиальная
часть которой
-состоянии описывается волновой функцией, радиальная
часть которой 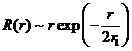 , где
, где ![]() - первый боровский
радиус. Найти в этом состоянии:
- первый боровский
радиус. Найти в этом состоянии:
а) наиболее вероятное расстояние ![]() электрона от ядра;
электрона от ядра;
б) среднее расстояние ![]() между электроном и
ядром.
между электроном и
ядром.
Решение:
Радиальная часть волновой функции электрона в атоме водорода
в ![]() -состоянии имеет вид:
-состоянии имеет вид:
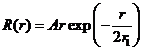 (1)
(1)
где ![]() - некоторая
постоянная, которую найдём, используя условие нормировки волновой функции:
- некоторая
постоянная, которую найдём, используя условие нормировки волновой функции:
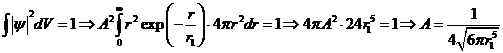 (2)
(2)
Таким образом, радиальная часть волновой функции электрона примет вид:
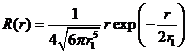 (3)
(3)
Физический смысл пси-функции состоит в том, что квадрат
модуля пси-функции определяет плотность вероятности местонахождения частицы. Тогда
вероятность нахождения частицы в шаровом слое радиуса ![]() и толщиной
и толщиной ![]() равняется:
равняется:
 (4)
(4)
Отсюда следует, что вероятность нахождения электрона в шаровом слое единичной толщины равняется:
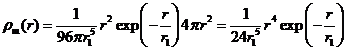 (5)
(5)
Найдём значение ![]() , при котором функция (5) имеет максимум:
, при котором функция (5) имеет максимум:
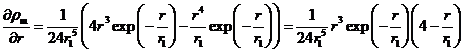 (6)
(6)
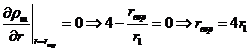 (7)
(7)
Графически зависимость (5) представлена на рисунке 1:
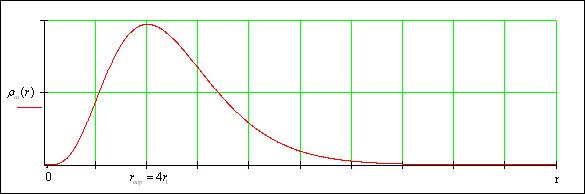
Рисунок 1
Таким образом, наиболее вероятное расстояние электрона от
ядра равняется ![]() .
.
В квантовой механике среднее значение физической величины ![]() в квантовом состоянии,
описываемом волновой функцией
в квантовом состоянии,
описываемом волновой функцией ![]() , определяется следующим выражением:
, определяется следующим выражением:
![]() (8)
(8)
где ![]() - функция, комплексно
сопряжённая к волновой функции
- функция, комплексно
сопряжённая к волновой функции ![]() ,
, ![]() - оператор физической
величины
- оператор физической
величины ![]() . В нашем случае
. В нашем случае ![]() ,
, ![]() , поэтому выражение (8) примет вид:
, поэтому выражение (8) примет вид:
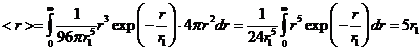 (9)
(9)
Таким образом, среднее расстояние между электроном и ядром
равняется ![]() .
.
Ответ: а) ![]() , б)
, б) ![]() .
.