Комптоновское смещение длины волны фотона определяется следующим соотношением:

(1)

где - длина волны падающего фотона, - длина волны рассеянного фотона, - комптоновская длина волны электрона (здесь - масса покоя фотона).

Отсюда длина волны смещённого фотона:

(2)

Импульс рассеянного фотона:

(3)

На рисунке 1 представлен рисунок треугольника импульсов при взаимодействии фотона и свободного электрона:

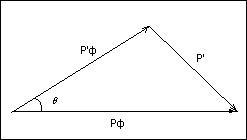
Рисунок 1

В соответствии с законом сохранения импульса: .

Модуль вектора импульса рассеянного фотона может изменяться в пределах от ( при - нерассеянный фотон максимальное значение модуля вектора импульса фотона) до ( при - минимальное значение модуля вектора импульса рассеянного фотона).

Найдём какие значения импульсов имеют фотоны рассеянные под углами от до . Найдём дифференциал для выражения (3):

(4)

Знак минус показывает лишь, что при увеличении угла модуль вектора импульса фотона уменьшается. Следовательно, для интервала углов рассеяния значение импульса рассеянного фотона изменяется в пределах от до . Считая распределение фотонов по импульсам равновероятным на всём промежутке изменения угла рассеяния, получим, что относительное число фотонов, рассеянных под углами от до , равняется:

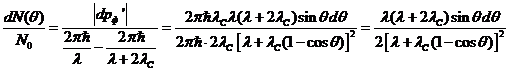(5)

Здесь - число падающих фотонов. Из выражения (5) следует, что:

(6)

Мы получили функцию плотности вероятности для числа рассеянных фотонов в зависимости от угла рассеяния. График этой функции (рисунок 2):

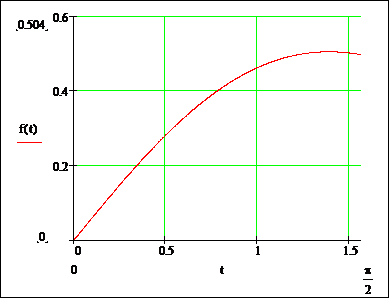
Рисунок 2

Действительно в интервале значений угла рассеяния эта функция возрастает, значит, при увеличении угла рассеяния от 0 до возрастает и число фотонов, рассеянных под этим углом.