Тепловое излучение.

1.1 Тепловое излучение и люминесценция.

Тепловое излучение – это излучение, которое возникает за счёт внутренней энергии тел. Излучение, возникающее по другим причинам, называется люминесценцией. Виды люминесценции:

1. хемилюминесценция – возникает вследствие химических реакций;
2. электролюминесценция – возникает в некоторых веществах, в которых создаётся электрическое поле;
3. катодолюминесценция – возникает при бомбардировке вещества пучком электронов;
4. фотолюминесценция – излучение вследствие поглощения электромагнитных волн.

Тепловое равновесие – это такое состояние системы, при котором распределение энергии между телом и веществом остаётся неизменным для каждой длины волны. Опыт показывает, что единственным видом излучения, которое может находиться в состоянии теплового равновесия с веществом, является тепловое излучение.

1.2 Закон Кирхгофа.

Энергетическая светимость – это энергия, которая излучается единицей поверхности излучающего тела в единицу времени в пределах телесного угла 2π стерадиан. Энергетическая светимость является функцией температуры. Пусть единица поверхности в единицу времени излучает в диапазоне частот от ω до dω энергию dR:

(1.1)

- испускательная способность тела. Таким образом энергетическая светимость:

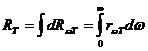(1.2)

Испускательная способность является функцией частоты и температуры. Излучение можно характеризовать вместо частоты длиной волны λ:

(1.3)

Тогда испускательная способность как функция длины волны и температуры:

(1.4)

Пусть на элементарную площадку dS падает поток электромагнитной энергии dФ, пусть dФ’ – поток электромагнитной энергии, поглощаемый этой площадкой. Поглощательной способностью тела называют отношение dФ’ и dФ:

(1.5)

Абсолютно чёрным телом называется тело, полностью поглощающее падающее на него излучение всех частот. Для такого тела . Для всех остальных тел . Закон Кирхгофа: отношение испускательной и поглощательной способностей тел не зависит от природы тела, а является для всех тел универсальной функцией от частоты и температуры.

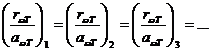(1.6)

Универсальная функция, равная отношению испускательной и поглощательной способностей тела, называется функцией Кирхгофа:

(1.7)

Если перейти к длине волны, то получим функцию:

(1.8)

(1.9)

1.3 Равновесная плотность энергии излучения.

Пусть - равновесная плотность энергии излучения, приходящаяся на интервал частот от до .Тогда плотность энергии излучения на всём диапазоне частот от 0 до ∞:

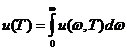(1.10)

Пусть R^* - энергетическая светимость абсолютно чёрного тела. Так как поглощательная способность абсолютно чёрного тела равна 1, то испускательная способность абсолютно чёрного тела рана функции Кирхгофа. Установим связь между универсальной функцией Кирхгофа и равновесной плотностью энергии излучения. На рисунке 1.1 dS – элементарная площадка на поверхности излучающего тела. Плотность потока энергии в этом случае будет определяться следующим образом:

(1.11)

где - телесный угол, соответствующий площадке, через которую определяют плотность потока энергии. Предположим, что площадка имеет прямоугольную форму. Из рисунка видно, что её стороны равны и . Тогда по определению телесного угла мы имеем:

(1.12)

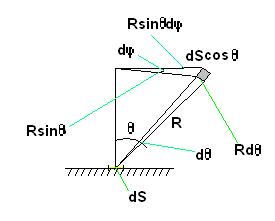
Рисунок 1.1

Тогда плотность потока энергии:

(1.13)

Найдём поток энергии через эту площадку:

(1.14)

Тогда поток энергии найдём интегрированием этого выражения по θ от 0 до 2π и по φ от 0 до π/2:

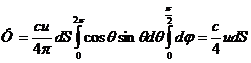(1.15)

Поток энергии можно найти также как произведение энергетической светимости на площадку dS:

(1.16)

Сравнив выражения (1.15) и (1.16) и сократив на dS, получим:, или, учитывая, что это соотношение должно выполняться для любой спектральной области:

(1.17)

1.4 Закон Стефана-Больцмана и закон Вина.

Закон Стефана-Больцмана: энергетическая светимость абсолютно чёрного тела пропорциональна 4-ой степени температуры тела:

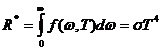(1.18)

где σ = 5.7∙10^-8 Вт/(м²∙К⁴) – постоянная Стефана-Больцмана.

Вин установил, что:

(1.19)

Используя формулу (1.9) перейдём к функции :

(1.20)

Установим длину волны , на которую приходится максимум функции :

(1.21)

(1.21)

Решая это уравнение, получим закон смещения Вина:

(1.22)

b = 2.90∙10^-3 м∙К – постоянная Вина.

1.5 Стоячие волны в пространстве трёх измерений.

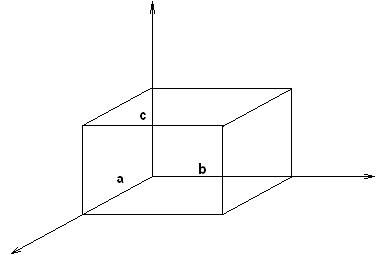
Рисунок 1.2

Рассмотрим некоторый объём, в котором распространяются волны, имеющие следующие уравнения:

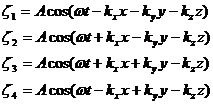
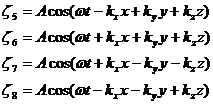(1.23)

В случае, когда отражение волны происходит без изменения фазы, уравнение стоячей волны имеет вид:

(1.24)

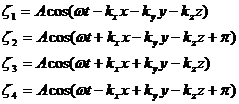
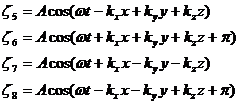(1.25)

В случае, когда волна при отражении претерпевает скачок фазы на π, уравнение стоячей волны имеет вид:

(1.26)

Из уравнений (1.24) и (1.26) следует, что для того, чтобы амплитуда имела одинаковое значение во всех 8 вершинах, необходимо выполнение условий:

(1.27)

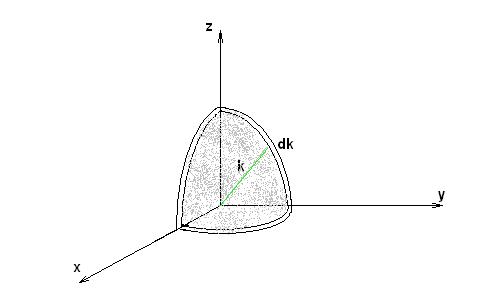
Рисунок 1.3

Объём, приходящийся на одну стоячую волну, , откуда плотность точек равна . Найдём число точек лежащих в пределах 1/8 шарового слоя (рисунок 1.3). Его объём равен . В этом случае число стоячих волн, проекции волновых векторов которых лежат в интервалах от k_x до k_x+dk_x, от k_y до k_y+dk_y, от k_z до k_z+dk_z:

(1.28)

С учетом того, что , имеем:

(1.29)

Так как число стоячих волн в данном объёме пропорционально объёму V, то для плотности полевых осцилляторов имеем выражение:

(1.30)

Для электромагнитных волн, имеющих одно направление , существуют две возможные плоскости поляризации, которые взаимно перпендикулярны, поэтому выражение (1.30) следует умножить на 2. Таким образом, с учётом возможных плоскостей поляризации, плотность полевых осцилляторов равна:

(1.31)

1.6 Формула Рэлея-Джинса.

Каждая колебательная степень свободы обладает энергией ,тогда энергия, приходящаяся на диапазон частот от ω до dω равна:

(1.32)

Тогда равновесная плотность излучения:

(1.33)

Учитывая соотношения (1.17) можно найти аналитический вид функции Кирхгофа:

(1.34)

Это формула Рэлея-Джинса. Она хорошо согласуется с опытом в диапазоне длинных волн и резко отличается в диапазоне коротких волн.

1.7 Формула Планка.

Планк предположил, что энергия передаётся порциями (квантами):

(1.35)

Соответственно энергия излучения пропорциональна величине :

(1.36)

Вероятность того, что энергия стоячей волны имеет значение :

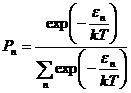(1.37)

Средняя энергия стоячей волны имеет значение, равное:

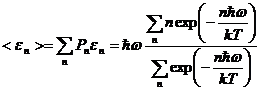(1.38)

Обозначим , тогда получим:

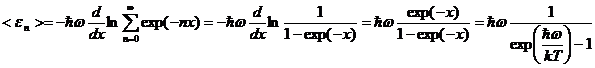
Это выражение для средней энергии полевого осциллятора. Учитывая формулу (1.31) для плотности полевых осцилляторов, найдём выражение для плотности энергии излучения, приходящейся на спектральный интервал от ω до d ω:

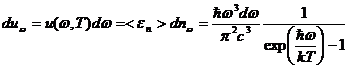(1.39)

Разделив обе части на dω, получим аналитическое выражение для функции :

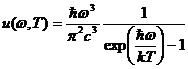(1.40)

Учитывая связь испускательной способности абсолютно чёрного тела со спектральной характеристикой плотности энергии излучения, найдём вид функции Кирхгоффа:

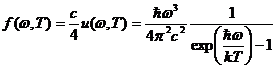(1.41)

График функции Кирхгофа представлен на рисунке 1.4.

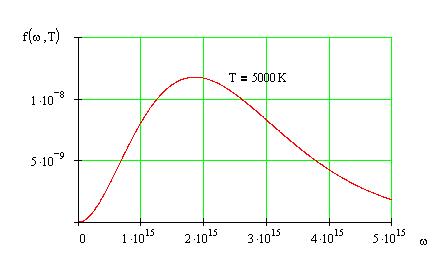
Рисунок 1.4

Найдём энергетическую светимость R^* абсолютно чёрного тела. Для этого необходимо вычислить интеграл:

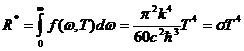(1.42)

Т.е. мы получили закон Стефана-Больцмана. Отсюда видно, что постоянная Стефана-Больцмана σ равна:

(1.43)

Значение, полученное по формуле (1.43), совпадает с экспериментальным. Перейдём к функции :

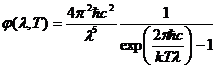(1.44)

Продифференцировав (1.62) по dλ, и приравняем производную к нулю, найдём условие максимума:

(1.45)

Мы получили закон Вина.