Задача 1.1.
Две гладкие частицы сферической формы с массами m1
и m2, движущиеся со скоростями 
и 
, сталкиваются под углом b, как указано на
рис.1
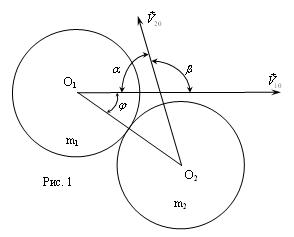
Расстояние до места встречи и скорости частиц
соответствуют условиям соударения (отсутствию промаха). На рис.1:
b — угол встречи, т.е. угол, образованный
векторами и ;
a = (p - b) — дополнительный угол;
j — угол между линией удара O1O2 и
вектором .
Другие обозначения:
и 
— скорости
соответственно 1-ой и 2-ой частицы после удара.
— совместная скорость частиц после абсолютно неупругого
удара.
q — угол отклонения частицы после удара, т.е. угол,
образованный векторами и или и .
g — угол разлета частиц после удара, т.е. угол,
образованный векторами 
и 
.
и 
— импульсы соответственно 1-ой и 2-ой частицы после удара.
E1, E2 — кинетические энергии соответственно 1-ой и 2-ой
частицы после удара.
DE
— изменение кинетической энергии механической системы, состоящей из двух частиц
за время удара.
Виды взаимодействия:
а) абсолютно упругий удар (АУУ);
б) неупругий удар (НУУ);
в) абсолютно неупругий удар (АНУУ).
Общие исходные данные: m*
= 10-3кг, V*
= 10 м/с, a* = p/2.
Другие данные:
|
№ вар |
Исходные данные к задаче 1-1 |
||||||
|
m1 |
m2 |
V10 |
V20 |
a |
j |
q |
|
|
2 |
m* |
1/2m* |
2V* |
0 |
- |
2/3a* |
- |
|
№ вар |
Вид взаимодействия |
Определить |
|||||||||||
|
АУУ |
НУУ |
АНУУ |
V1 |
V2 |
g |
E1 |
E2 |
q |
p1 |
p2 |
DE |
U
|
|
|
2 |
+ |
- |
- |
- |
- |
- |
+ |
+ |
+ |
- |
- |
- |
- |
В нашем случае удар абсолютно упругий. До соударения вторая частица покоилась.
Рисунок 1 в нашем случае имеет вид:
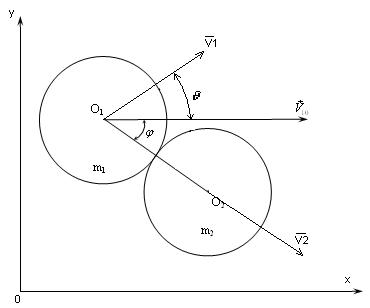
Рисунок 2
Решение:
Так как удар в нашем случае абсолютно упругий, то по закону сохранения импульса имеем:
(1)
Используя закон сохранения энергии, получим:
(2)
Введём систему координат так, как показано на рисунке 2.
Учитывая, что 
- угол между вектором 
и осью, соединяющей
центры частиц OO1, а 
- угол разлёта частиц
после соударения, запишем закон сохранения импульса в нашем случае в проекциях
на оси ox и oy:
(3)
Таким образом, объединяя уравнения (2) и (3), получим систему:
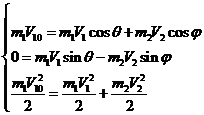(4)
Из первого уравнения системы (4) получим:
(5)
Возведём обе части уравнения (5) в квадрат:
(6)
Из второго уравнения системы (4) получим:
(7)
Возведём обе части уравнения (7) в квадрат:
(8)
Сложим уравнения (6) и (8) и получим:
(9)
(10)
Умножим обе части третьего уравнения системы (4) на 
и получим:
(11)
Подставим выражение (10) в уравнение (11):
(12)
Решая это квадратное уравнение относительно 
, получим 
или 
. Решение соответствует
отсутствию соударения, поэтому скорость второй частицы после соударения:
(13)
Подставим в третье уравнение системы (4) и получим:
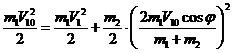
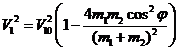(14)
Отсюда получим:
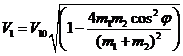(15)
Отрицательное решение уравнения (15) в нашем случае смысла не имеет:
Из второго уравнения системы (4) получим:
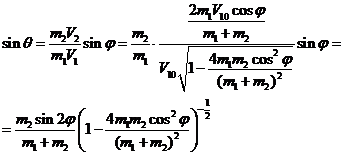(16)
Отсюда угол отклонения частицы после удара:
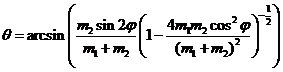(17)
Подставляя числовые значения, получим:
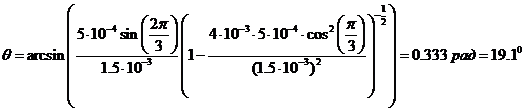
Найдём кинетические энергии частиц после соударения:
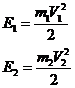(18)
Подставляя выражения (13) и (15) в выражения (18), получим:
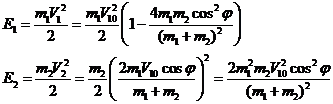(19)
Подставляя числовые значения, получим:
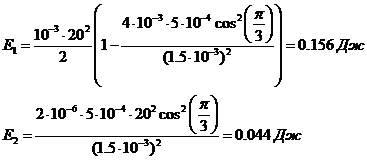
Ответ:
Угол отклонения первой частицы в результате соударения:
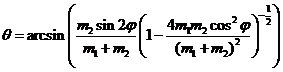
Кинетические энергии частиц поле соударения:
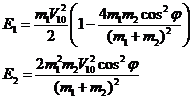
